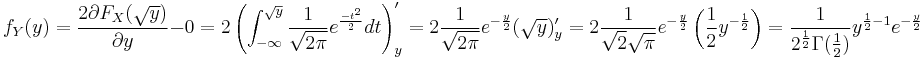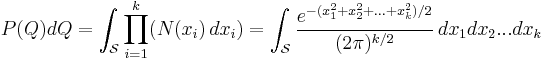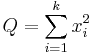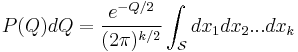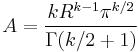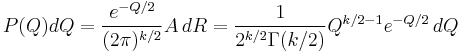Proofs related to chi-squared distribution
The following are proofs of several characteristics related to the chi-squared distribution.
Contents |
Derivations of the pdf
Derivation of the pdf for one degree of freedom
Let random variable Y be defined as Y = X2 where X has normal distribution with mean 0 and variance 1 (that is X ~ N(0,1)).
Then if  and if
and if 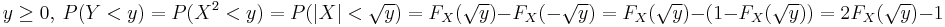
Where  and
and  are the cdf and pdf of the corresponding random variables.
are the cdf and pdf of the corresponding random variables.
Then 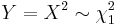 .
.
Derivation of the pdf for two degrees of freedom
To derive the chi-squared distribution with 2 degrees of freedom, there could be several methods. Here presented is one of them which is based on the distribution with 1 degree of freedom.
let  and
and  are two independent variables and satisfy that
are two independent variables and satisfy that 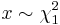 and
and 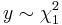 , thus, the probability density functions of
, thus, the probability density functions of  and
and  are respectively:
are respectively:
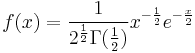 and
and 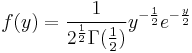
Simply, we can derive the joint distribution of  and
and  :
:
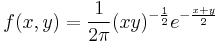
where 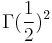 is replaced by
is replaced by  . Further, let
. Further, let 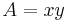 and
and 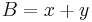 , we can get that:
, we can get that:
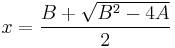 and
and 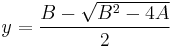
or, inversely
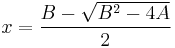 and
and 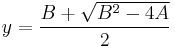
Since the two variable change policies are symmetric, we take the upper one and multiply the result by 2. The Jacobian determinant can be calculated as:
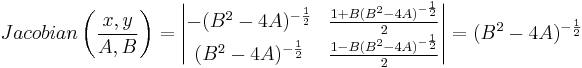
Now we can change 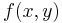 to
to 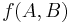 :
:
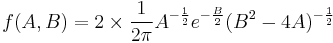
where the leading constant 2 is to take both the two variable change policies into account. Finally, we integrate out  to get the distribution of
to get the distribution of  , i.e.
, i.e.  :
:
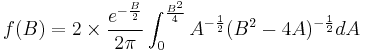
Let 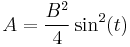 , the equation can be changed to:
, the equation can be changed to:
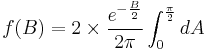
So the result is:
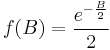
Derivation of the pdf for k degrees of freedom
Consider the k samples  to represent a single point in a k-dimensional space. The chi square distribution for k degrees of freedom will then be given by:
to represent a single point in a k-dimensional space. The chi square distribution for k degrees of freedom will then be given by:
Where 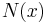 is the standard normal distribution and
is the standard normal distribution and 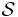 is that k-1 dimensional surface in k-space for which
is that k-1 dimensional surface in k-space for which
It can be seen that this surface is the surface of a k-dimensional ball or, alternatively, an n-sphere where n=k-1 with radius 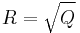 , and that the term in the exponent is simply expressed in terms of Q. Since it is a constant, it may be removed from inside the integral.
, and that the term in the exponent is simply expressed in terms of Q. Since it is a constant, it may be removed from inside the integral.
The integral is now simply the surface area A of the k-1 sphere times the infinitesimal thickness of the sphere which is
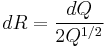 .
.
The area of a k-1 sphere is:
Substituting, realizing that 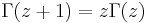 , and cancelling terms yields:
, and cancelling terms yields: